Wavelet Applications in Signal processing
Sharp Transition/ Discontinuities Detection
Wavelets are short duration mathematical functions that can be dilated and translated along a given signal and thus have the capability to analyze a signal at different scales. This makes them ideally suited for detecting short duration rapid variations in the signal in the form of discontinuities and singularities.
Discontinuities can be detected using either continuous or discrete wavelet transforms. Example using continuous and discrete transforms utilizing db2 wavelet follows.
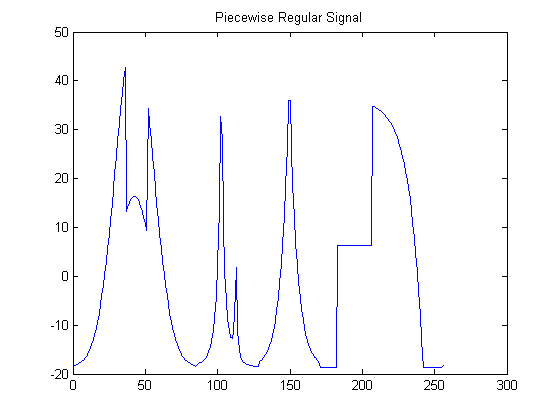
N=256 Piecewise regulat Signal
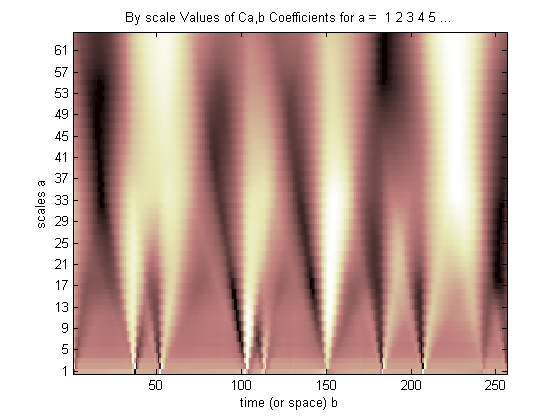
Continuous Wavelet Transform of Signal Using Db2 Wavelet
First, let us consider continuous transform. In this example 64 scale levels are utilized. Since scales are inversely proportional to frequency, the scales at the lowest end of the figure correspond to highest frequencies and vice-versa.The lighter colors correspond to higher coefficients. We see high coefficients value near sharp transitions and the effect is much more pronounced at lower scales (higher frequencies) as these high frequencies match with sharp transitions. The inner product between scaled/dilated wavelet and a portion of signal yields the largest coefficients where the signal has similar spectral components as the wavelet. Coefficients are calculated as following
\[ C_{a,b}= \lt f,\psi_{a,b} \gt =\int_{-\infty}^\infty\!f(t)\frac{1}{\sqrt{a}}\psi^*(\frac{t-b}{a})\,dt \]The mother wavelet (Db2) in this case is scaled and for that scale value it is translated along the signal length and coefficients are calculated at every point.The scale value is changed and the process is repeated. The practical implementation involves using discrete values of translation steps and scaling values but large enough step values approximates CWT well.
A \(3D\) display of coefficients distribution along scales and signal length is shown in the figure below. It can be seen that at higher frequencies CWT does a very good job of isolating sharp transitions.

Continuous Wavelet Transform of signal using Db2 wavelet(3D view)
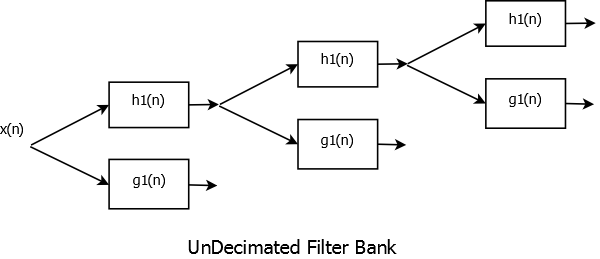
Undecimated Filter Bank
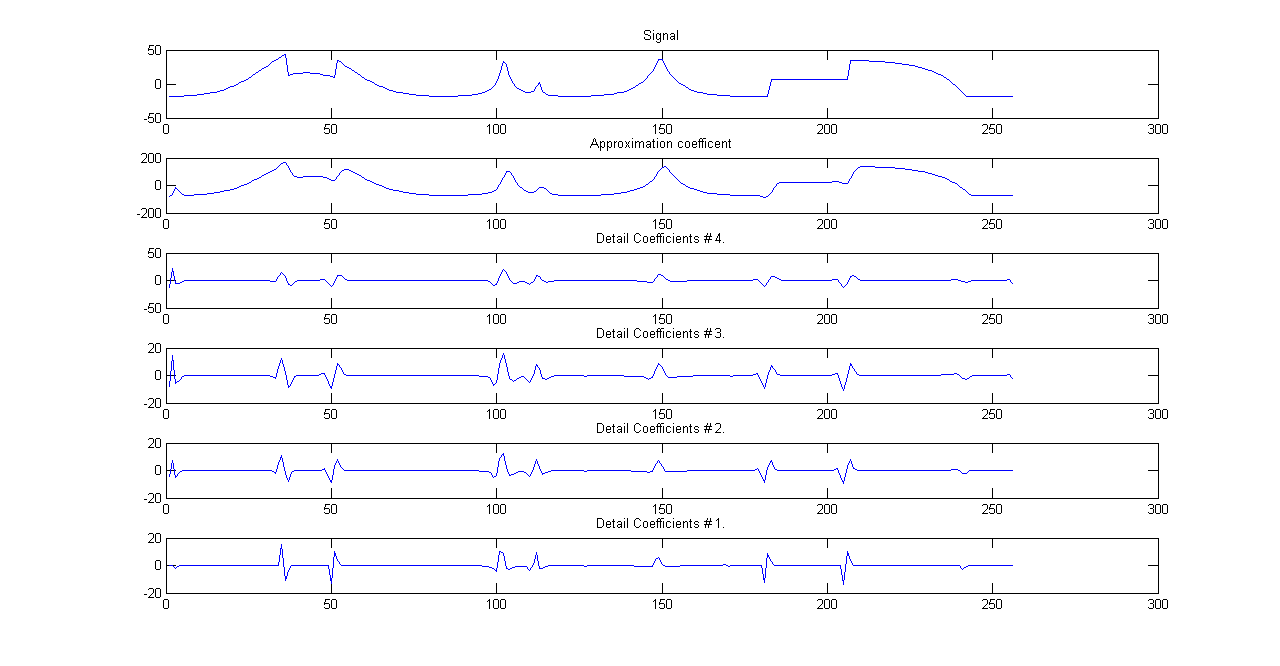
4-level Discrete Wavelet Transform of signal using Db2 wavelet
Discrete Wavelet Transform is computed a little differently considering we use filter banks and dyadic scale values but it still does a good job of isolating sharp transitions. We usually use undecimated filter banks in determining presence and location of discontinuities/transitions as coefficients storage for signal reconstruction is not a crucial issue. We get detail coefficients after convolving with high pass filters and approximation coefficients after filtering with low pass filters. If we are resolving the signal to \(J=4\) scales, we have one approximation set of coefficients at 4th scale while four sets of detail coefficients. In the DWT display of signal, approximation and detail coefficients we move from coarser scales down to finer scales (higher frequencies). As can be seen from the figures, sharp transitions are isolated best at the highest frequencies.
Signal Denoising
DWT is implemented by iterating along the low pass channel of designed filter banks and we take out high frequency components at every stage. This kind of set-up is specially useful when dealing with noise as it usually consists of higher frequency components. In the following figures, an example of denoising is shown. The signal is a doppler with frequencies decreasing in time. DWT filters out higher frequencies from the signal in every successive stage. After \(4\) stages of filtering we have an approximation of the original signal. It is seen that DWT does a good job with lower frequencies while higher frequencies of the signal (at the beginning of the signal) get chopped down along with the noise. DWT performs substantially better with smoother noise-contaminated signals.
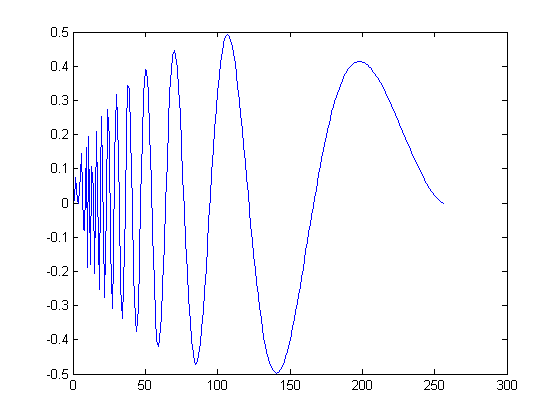
Doppler Signal
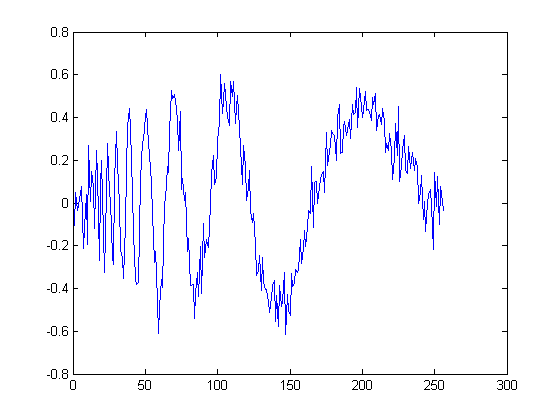
Doppler Signal with AWGN

4-level of Discrete Wavelet Transform of Noisy Signal using Db2 wavelet
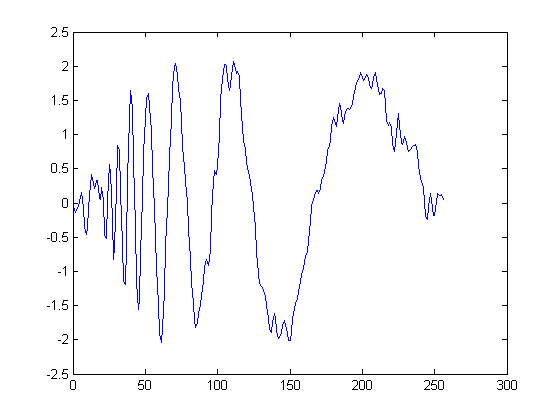
Denoised signal
