Filter Design for Wavelets
For two channel filter banks, perfect reconstruction equations are given by \[ \frac{1}{2}(H_{1}(z)H_{2}(z)+G_{1}(z)G_{2}(z))= z^{-L} \] and \[ \frac{1}{2}(H_{1}(-z)H_{2}(z)+G_{1}(-z)G_{2}(z)) = 0 \]
First equation is called the no-distortion equation while second one is no aliasing condition. For filter design we focus mainly on the first equation. \(H_{1}(z)\) and \(H_{2}(z)\) are analysis and synthesis low pass filters while \(G_{1}(z)\) and \(G_{2}(z)\) are high pass filters. For perfect reconstruction, it is sufficient to design low pass filters and obtain high pass filters from them.
Let \(P(z)\) be the product filter of the two low pass filters.
\[ P(z)=H_{1}(z)H_{2}(z) \]Three steps are needed to design the perfect reconstruction filter bank
- 1. Design Low Pass Filter \(P(z)\).
- 2. Factorize \(P(z)\) to find \(H_{1}(z)\) and \(H_{2}(z)\).
- 3. Use PR conditions to obtain high pass filters from low pass filters.
Step 3 is trivial once the low pass filters are obtained. Choose \(H_{2}(z)=G_{1}(-z)\) and \(G_{2}(z)=-H_{1}(-z)\) for alias cancellation. Plugging this in first PR equation we get
\[ \frac{1}{2}(H_{1}(z)H_{2}(z)-H_{2}(-z)H_{1}(-z))= z^{-L} \] \[ P(z)-P(-z)= 2z^{-L} \]It can be seen from the equation above that all odd powers of \(P(z)\) will cancel out. If we redefine \(P(z):=z^{-L}P(z)\), the equation changes to \[ z^{-L}P(z)-(-z)^{-L}P(-z)=2z^{-L} \] or, \[ P(z)+P(-z)=2 \]
This is done to center the equation so that the coefficient of the term \(z^{0}\) is non-zero. Filter \(P(z)\) is known as halfband filter. All of its even terms, with the exception of \(z^{0}\) are zero. When we add \(P(z)\) with \(P(-z)\) we are left with a constant 2.[ Remember that only odd terms will cancel out with the addition so if there is an even term present it will appear in the output ].Furthermore, \(P(z)\) is a product of two low pass filters.
In orthogonal case, \[ P(z)=H_{1}(z)H_{1}(z^{-1})=H_{1}(e^{j\omega})H_{1}(e^{-j\omega}) \] which can be seen as an autocorrelation function because in time domain, the two filters are time reversed versions of each other. eg., \(1+az^{-1}+bz^{-2}+cz^{-3}\) and \(1+az^{1}+bz^{2}+cz^{3}\) have coefficents \([1,a,b,c]\) and \([c,b,a,1]\).
In the case where the two low pass filters are ``different'' (one cannot be obtained from other just by reversing the filter order) ,as in biorthogonal filter bank, the product \(P(z)\) can be seen as a cross-correlation function. It will still be a low pass filter in both cases.
There are a number of halfband filter design and factorization methods. Daubechies and Meyer's methods are more commonly used.
Daubechies Method: Daubechies defined P as \(2(1-y)^{p}B_{p}(y)\) where \(B_{p}(y)\) is a truncated Binomial polynomial of degree \((p-1)\) and \(p\) coefficients. \[ B_{p}(y)=(1-y)^{-p}=1+py+\frac{p(p+1)}{2}y^{2}+....+(\begin{array}{ccc}2p-2\\p-1\end{array})y^{p-1} \] The coefficient of \(y^{k}\) is \((\begin{array}{ccc}p+k-1\\k\end{array})\). The factor \((1-y)^{p}\) has \(p\) zeros at \(y=1\). In Low Pass filter case, we want zeros at \(z=-1\) or \(\omega=\pi\). Let \[ y=\frac{(1-e^{-j\omega})}{2}\frac{(1+e^{-j\omega})}{2} \] in order to maintain symmetry \[ y=(\frac{1-cos\omega}{2}) \] which gives \[ P(\omega)=2(\frac{1+cos\omega}{2})^{p}\sum_{k=0}^{p-1}(\begin{array}{ccc}p+k-1\\k\end{array})(\frac{1-cos\omega}{2})^{k} \]
In z-domain this can be written as \[ P(z)=2(\frac{1+z}{2})^{p}(\frac{1+z^{-1}}{2})^{p}\sum_{k=0}^{p-1}(\begin{array}{ccc}p+k-1\\k\end{array})(\frac{1-z}{2})^{k}(\frac{1-z^{-1}}{2})^{k} \] \(P(z)\) can be obtained for different values of p. Once we have P(z), the next step is to factorize it in order to obtain the low pass filters.
Meyer's Method: It consists of integrating \(P'(\omega)\) and choosing a value c such that \(P(\pi)=0\).It is given by \[ P(\omega)=2-c\int_{0}^{\omega} (sin(\omega))^{2p-1} d\omega \]
Plots of \(P(\omega)\) for values of \(p=1,2,3\)
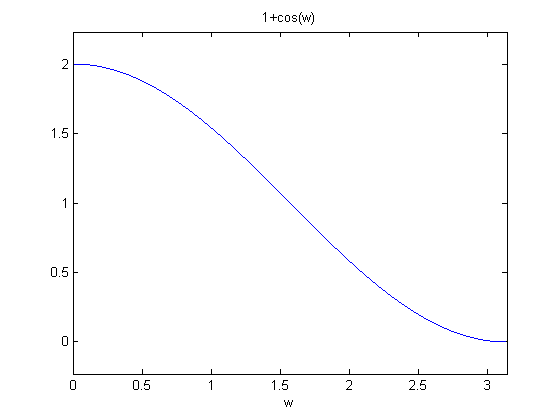
\(P(\omega\)) for p=1
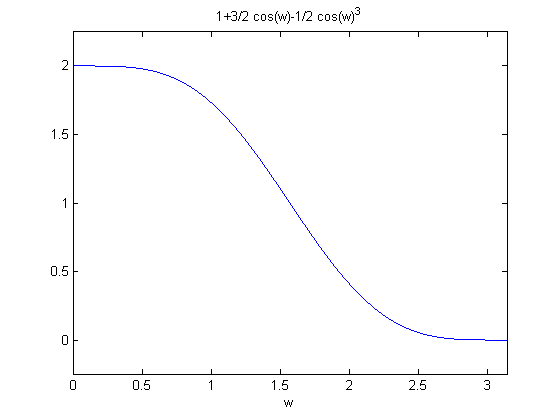
\(P(\omega\)) for p=2
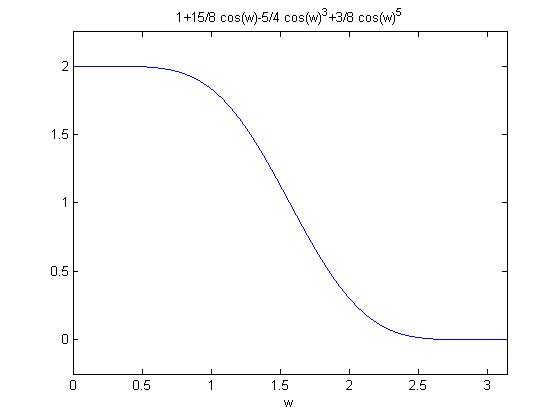
\(P(\omega\)) for p=3
Spectral factorization
Once we have \(P(z)\), the next step is to find low pass filters. In the orthogonal case \(P(z)=H(z)H(z^{-1})\). As seen above \(P(z)\) can be re-written as
\[ P(z)=[(1+z)^{p}(1+z^{-1})^{p}Q(z)] \]The value of \(Q(z)\) comes from binomial expansion and , looking at these equations, it makes sense to factorize \(Q(z)\) as \(Q(z)=R(z)R(z^{-1})\). Daubechies suggested that \(H(z)\) be chosen such that it is minimum phase which will make \(H(z^{-1}\) maximum phase. Therefore, \(R(z)\) must be chosen to be causal and with all its zeros inside the unit circle. For example, consider the product filter for p=2. Its pole-zero plot as obtained using Matlab is shown below.
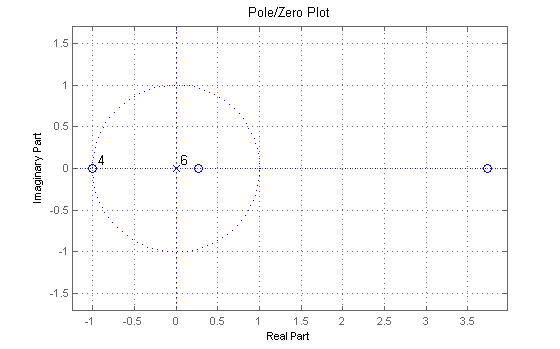
Pole zero plot of \(P(\omega\) for p=2
There are four zeros at \(z=-1\). For orthogonal filters, we need to assign them equally to \(H(z)\) and \(H(z^{-1})\).
\[ P(z)=(\frac{-1}{16}z^{3}+\frac{9}{16}z^{1}+1+\frac{9}{16}z^{-1}+\frac{9}{16}z^{-3}) \]This can be expressed as
\[ P(z)=\frac{1}{16}(1+z)^{2}(1+z^{-1})^{2}(-z+4-z^{-1}) \]As can be seen from the equation and pole-zero plot. This has \(4\) zeros at \(z=-1\). The other two zeros are at \(2-\sqrt{3}\) and \(2+\sqrt{3}\). \(H(z)\) is assigned the zero inside the unit circle while \(H(z^{-1})\) takes zeros from outside the unit circle. Calculating coefficients using roots function of matlab gives us four coefficients for analysis low pass filter \(h(n)=[0.3415, 0.5915, 0.1585, -0.0915]\). The synthesis low pass filter is time reversed \(h(-n)=[-0.0915, 0.1585, 0.5915, 0.3415]\). The analysis and synthesis high pass filters can be calculated by alternate flipping the low pass coefficients and they are found to be \([-0.0915, -0.1585, 0.5915, -0.3415]\) and \([0.3415, -0.5915, 0.1585, 0.0915]\). The scaling and wavelet functions can be calculated using iteration method. They are below.
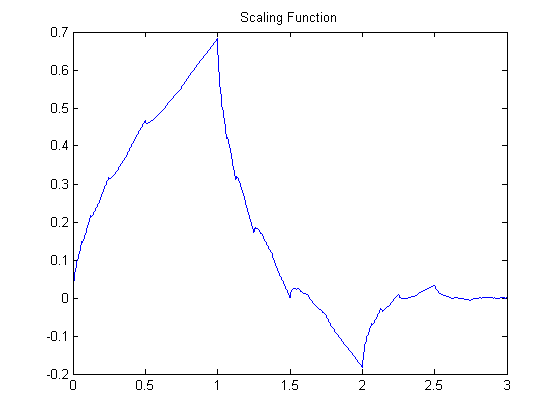
Scaling Function for Db2 wavelets(p=2)
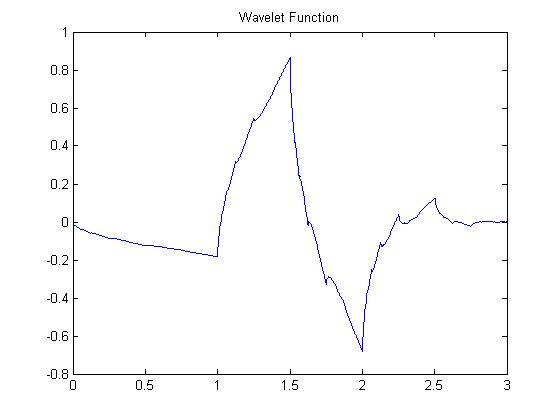
Wavelet Function for Db2 wavelets(p=2)
Filters for Biorthogonal Wavelets
Recall that we'll need two filters in this case and one of the requirement is that filters be linear phase. We can use same product filter \(P(z)\) in previous example and factor it accordingly to suit our goals. Obviously \(P(z)\) can be factored in a number of ways but one of the more commonly used factorization is designing one filter with two zeros at \(z=-1\) and the other filter contains other four zeros.
\[ H_{1}(z)=\frac{1}{4}(1+z^{-1})^{2} \]and
\[ H_{2}(z)=-\frac{1}{4} (1+z^{-1})^{2} (2+\sqrt(3)-z^{-1})(2-\sqrt(3)-z^{-1}) \]Looking at it from discrete time-domain angle, the first filter is a ``hat function'', a symmetric filter with coefficients \([1,2,1]/4\) and the other filter is a convolution between \([1,2,1]/4\) and \([-1 ,4, -1]/2\). The second filter has the coefficients \([-0.1250, 0.2500, 0.7500, 0.2500, -0.1250]\). It is easy to see that both filters are symmetric, linear phase filters. We can obtain the two corresponding high pass filters using perfect Reconstruction condition. Using Matlab, they are found to be \([0.2500, -0.5000, 0.2500]\) and \([0.1250, 0.2500, -0.7500, 0.2500, 0.1250]\) This biorthogonal filter bank is usually known as \(5/3\) filter bank because of the length of th two filters ( 3 and 5 taps, respectively). The scaling and wavelet functions associated with these filters are calculated by iterating these filters over their respective dilation equations and they are plotted as following.
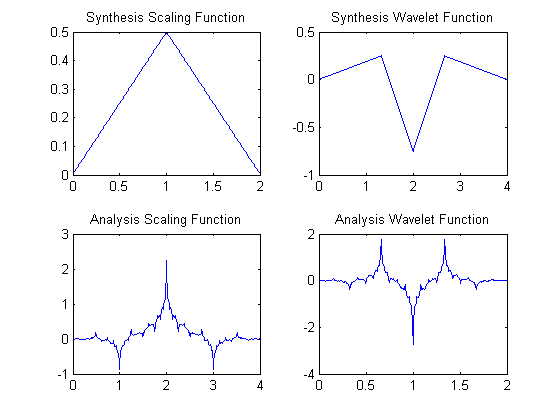
Wavelet and Scaling Functions for 5/3 Biorthogonal Filters (p=2)
Lifting Scheme: Haar Decomposition
Haar Decomposition is the most basic form of wavelet decomposition which essentially decomposes a signal into its average(Low Pass) and difference(High Pass).The signal \(s_{j+1,k}\) at scale \(j+1\) is decomposed into approximated signal \(s_{j,k}\) and a detail part \(d_{j,k}\) which is stripped away from the original signal.
\[ s_{j,k}=\frac{s_{j+1,2k}+s_{j+1,2k+1}}{2} \] \[ d_{j,k}=s_{j+1,2k+1}-s_{j+1,2k} \] or the average \(s_{j,k}\) can be written as \[ s_{j,k}=s_{j+1,2k}+\frac{d_{j,k}}{2} \]which is the even value of the signal added to half the difference between even and odd values of signal. In other words, if we calculate the difference first, we can calculate the average using only even values of the signal.
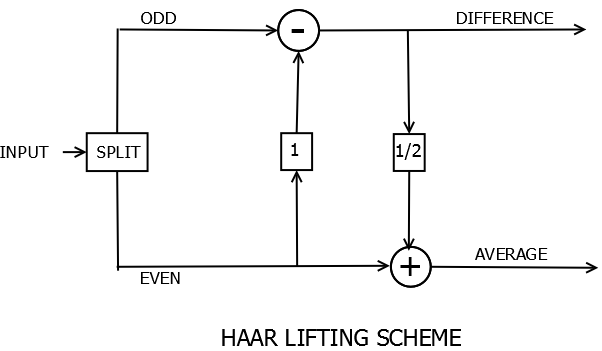
Haar Decomposition using Lifting Scheme
- 1. Split: Signal is split into even and odd components.
- 2. Predict: We use predict matrices P that work only on one half (even) of the signal and replace odd part with the difference or detail of the signal. In other words, we are trying to predict odd values using even values.
- 3. Update: The update matrices U update the even part by processing the difference part with U. Update is needed to preserve certain scalar quantities like average.
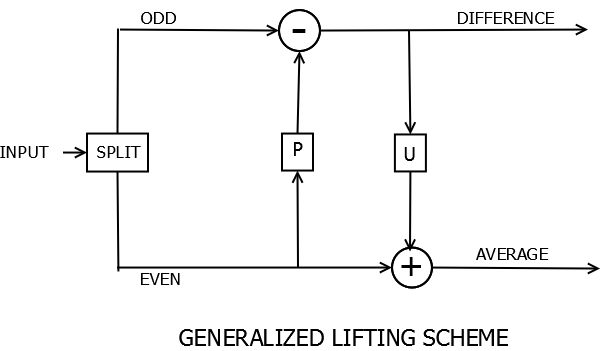
Generalized Lifting Scheme
Properties of Lifting Scheme
- 1. In-Place calculations: As can be seen from block diagrams, there is no reason to keep both even and odd components of the signal. We can simply replace odd values with the output after prediction. This idea can be extended when dealing with multi-stage lifting scheme. We can keep replacing inputs of any given branch with outputs and compute next stages as we go.
- 2. Invertibility: This is, of course, the most important property which makes lifting scheme useful in calculating wavelet transforms. As can be seen from the Haar example, the odd values of the input signal can be obtained by using even values and he difference values. In multistage lifting scheme inversion, we start from the last stage and keep inverting systematically until we recover the input. Inverted Lifting Scheme is shown below.
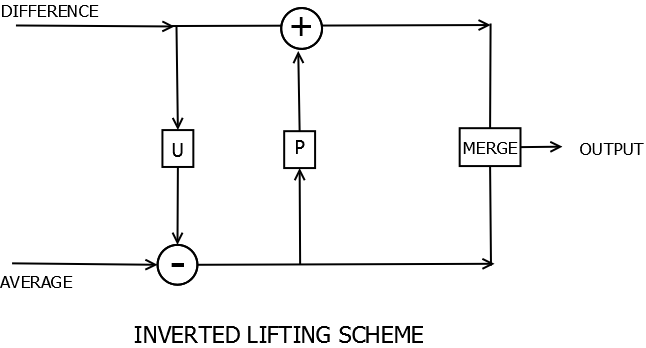
Generalized Inverted Lifting Scheme
Constructing Biorthogonal Wavelets using Lifting Scheme
Consider a Biorthogonal Filter Bank with
Low Pass Analysis Filter \(\widetilde{H_{j}}\)
High Pass Analysis Filter \(\widetilde{G_{j}}\)
Low Pass Synthesis Filter \(H_{j}\)
High Pass Synthesis Filter \(G_{j}\)
With lifting, the new filters are given by
\[ H_{j}^{new}=H_{j} \] \[ \widetilde{H_{j}^{new}}=\widetilde{H_{j}}+S_{j}\widetilde{G_{j}} \] \[ G_{j}^{new}=G_{j}-S_{j}^{*}H_{j} \] \[ \widetilde{G_{j}^{new}}=\widetilde{G_{j}} \]where \(S_{j}\) is a lifting operator which can be seen as equivalent to update operator U.
For these new filters to work, they must satisfy perfect reconstruction property. \[ \widetilde{H_{j}^{new}}(z)H_{j}^{new}(z)+\widetilde{G_{j}^{new}}(z)G_{j}^{new}(z)=2 \] and \[ \widetilde{H_{j}^{new}}(-z)H_{j}^{new}(z)+\widetilde{G_{j}^{new}}(-z)G_{j}^{new}(z)=0 \]
In Matrix notation,
$$\left(\begin{array}{ccc} \widetilde{H_{j}^{new}} \\ \widetilde{G_{j}^{new}}\end{array}\right)=\left(\begin{array}{ccc} 1 & S_{j}\\0 & 1 \end{array}\right) \left(\begin{array}{ccc}\widetilde{H_{j}} \\ \widetilde{G_{j}} \end{array}\right) $$ $$\left(\begin{array}{ccc} H_{j}^{new} \\ G_{j}^{new} \end{array}\right)=\left(\begin{array}{ccc} 1 & 0 \\-S_{j}^{*} & 1 \end{array}\right) \left(\begin{array}{ccc} H_{j} \\ G_{j} \end{array}\right) $$Multiplying first equation on both sides with conjugate transpose of the second equation on both sides. The product of two \(S_{j}\) matrices is, therefore
$$\left(\begin{array}{ccc} 1 & S_{j}\\0 & 1 \end{array}\right)\left(\begin{array}{ccc} 1 & -S_{j} \\0 & 1 \end{array}\right)=\left(\begin{array}{ccc} 1 & 0\\0 & 1 \end{array}\right)$$which corresponds to perfect reconstruction condition.
In time-domain, these four filter equations can be written as
\[ h_{j}^{new}(n)=h_{j}(n) \] \[ \widetilde{h_{j}^{new}}(n)=\widetilde{h_{j}}+\sum_{k} s_{j}(k)\widetilde{g_{j}}(n-k) \] \[ g_{j}^{new}(n)=g_{j}-\sum_{k} s_{j}^{*}(k)h_{j}(n-k) \] \[ \widetilde{g_{j}^{new}}(n)=\widetilde{g_{j}}(n) \]Tt can be seen from the equations that \(\widetilde{g_{j}}(n)\) and \(h_{j}^{new}(n)\) are unchanged. In order to find new wavelets and new scaling function we'll utilize dilation equations.
Analysis Dilation Equations
\[ \widetilde{\phi}(t)=2\sum_{k} \widetilde{h}(k)\widetilde{\phi}(2t-k) \] \[ \widetilde{\psi}(t)=2\sum_{k} \widetilde{g}(k)\widetilde{\phi}(2t-k) \]Synthesis Dilation Equations
\[ \phi(t)=2\sum_{k} h(k)\phi(2t-k) \] \[ \psi(t)=2\sum_{k} g(k)\phi(2t-k) \]Since low pass synthesis filter is unchanged, the new scaling function associated will also be unchanged.
\[ \phi^{new}(t)=\phi(t) \]However, new wavelet function for synthesis side is as follows
\[ \psi^{new}(t)=2\sum g^{new}(n)\phi(2t-n) \]Plugging value of \(g^{new}(n)\) gives us the following \[ \psi^{new}(t)=2\sum g(n)\phi(2t-n)-\sum_{k} \sum s^{*}(k)h(n'-k))\phi(2t-n) \] or, \[ \psi^{new}(t)=\psi(t)-\sum_{k} s^{*}\phi(t-k) \] Computing similarly we'll get \(\widetilde{\phi^{new}(t)}\) and \(\widetilde{\psi^{new}(t)}\). \[ \widetilde{\phi^{new}(t)}=2\sum \widetilde{h}(n)\widetilde{\phi^{new}}(2t-n) +2\sum s(k)\widetilde{\psi^{new}}(t-k) \] and \[ \widetilde{\psi^{new}(t)}= 2\sum \widetilde{g}(n)\widetilde{\phi^{new}}(2t-n) \]
The Lifted Wavelet Transform along with its inverse is shown in figure. The transform consists of primal lifting and dual lifting.
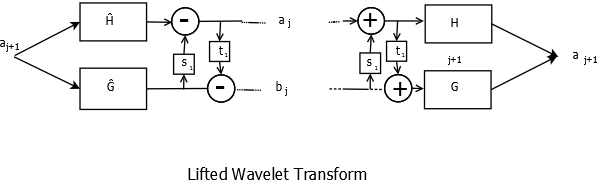
Forward and Reverse Lifted Wavelet Transform
where \(H(z)=H_{e}(z^{2})+z^{-1}H_{o}(z^{2})\) with even and odd parts separated and \(G(z)=G_{e}(z^{2})+z^{-1}G_{o}(z^{2})\)
If new filter is given by \(G^{new}(z)=G(z)+S(z^{2})H(z)\) then \(S(z^{2})H(z)\) can be given by polyphase \(H_{e}(z)S(z)\) and \(H_{o}(z)S(z)\). Therefore, the new polyphase matrix is
$$P^{new}(z)=P(z) \left(\begin{array}{ccc} 1 & S(z) \\ 0 & 1\end{array}\right)$$For dual lifting, the equation is \(H^{new}(z)=H(z)+T(z^{2})G(z)\). Proceeding as above, new filter polyphase matrix is given just for dual lifting is
$$P^{new}(z)=P(z) \left(\begin{array}{ccc} 1 & 0 \\ T(z) & 1\end{array}\right)$$Since we are using both primal and dual lifting in the same circuit, the new polyphase on the analysis side will be
$$\widetilde{P^{new}(z)}=\widetilde{P(z)} \left(\begin{array}{ccc} 1 & S(z) \\ 0 & 1\end{array}\right)\left(\begin{array}{ccc} 1 & 0 \\ T(z) & 1\end{array}\right)$$Next assume that we are using \(m\)-level cascade of primal and dual lifting then the new polyphase will be a product of \(m\) primal and dual matrices. Wim Sweldens and Ingrid Daubechies proved that using this method and starting with ``Lazy wavelet'' every finite wavelet transform can be obtained this way. A Lazy wavelet filter bank is one with \(H(z)=1\) and \(G(z)=z^{-1}\).
$$\widetilde{P^{new}(z)}=\left(\begin{array}{ccc} K_{1} & 0 \\ 0 & K_{2}\end{array}\right) \prod_{i}\left(\begin{array}{ccc} 1 & S_{i}(z) \\ 0 & 1\end{array}\right)\left(\begin{array}{ccc} 1 & 0 \\ T_{i}(z) & 1\end{array}\right)$$To see examples of designing filter banks with lifting scheme check this link. More examples are available at Wim Swelden's page. These two papers[Link 1,Link2] are essential reading.
. For software implementation, see this page.