Digital FIR Filters
A digital filter is a system that processes a digital signal. In 1-D the filtering process usually consists of removing or enhancing certain bands of frequency.
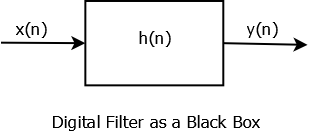
Digital Filter
In the figure above \( h(n) \) is the filter transfer function while \(x(n)\) and \(y(n)\) are input and output signals, respectively.
Finite Impulse Response (FIR) Filters
FIR filters have an impulse response that persists for only a finite number of samples and it is given by \[ h(n)=[h(0),h(1),......,h(N-1)] \] The output response of this filter is given by \[ y(n)=\sum_{k=0}^{N-1} x(k)h(n-k) \]
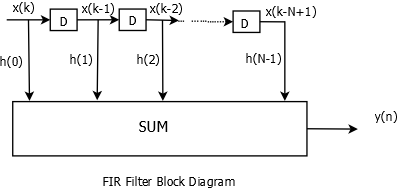
FIR Filter Block Diagram
Linear Phase FIR filters
Frequency response of any digital filter can be expressed in a magnitude-phase form. \[ H(\exp j\omega)=\|H(\omega)\|\angle\phi(\omega) \] A Linear Phase filter is one whose phase \(\omega\) is linear \[ \phi(\omega)=A\omega+B \]
A Linear Phase filter delays all frequency components equally (group delay) and it is highly desirable in phase-sensitive applications like image processing. Linear phase FIR filters can be easily designed by using symmetric impulse response. Following is a five tap FIR filter with coefficients \[[-0.125 , 0.250,0.750,0.250,-0.125]\] and its magnitude-phase response.
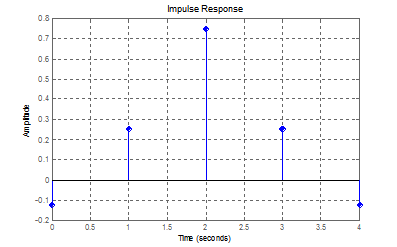
FIR Impulse Response
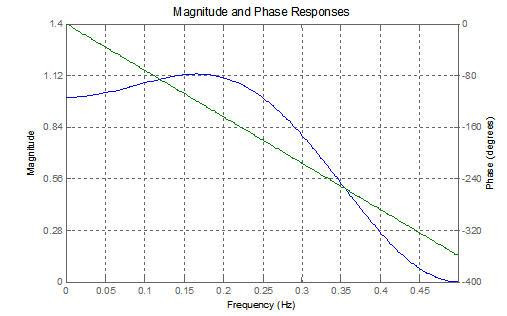
FIR Magnitude-Phase Response
