Wavelets: A Short Introduction
Wavelets are normalized,finite, short-duration, zero mean functions. $$\int_{-\infty}^\infty\psi(t)\,dt=0$$ \(\psi(t)\) is also known as Mother wavelet as it can be dilated and translated to yield Child wavelets. Function to be analyzed is then processed with these Children wavelets to yield wavelet coefficients.An example of a wavelet function is shown below. It is a Daubechies2 wavelet generated using Matlab.
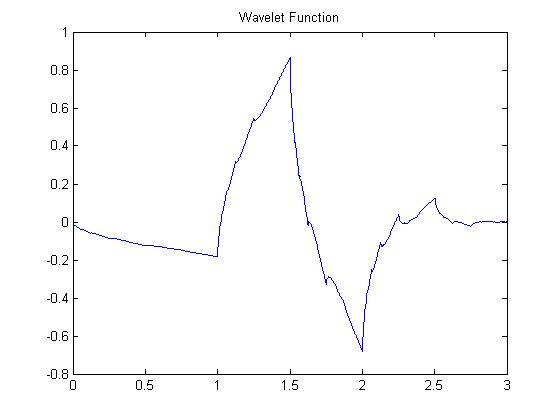
Db2 Wavelet
The Children wavelets are given by \(\psi_{k,s}(t)\) where the mother wavelet is scaled by s and translated by k. $$\psi_{k,s}(t)=\frac{1}{\sqrt{s}}\psi(\frac{t-k}{s})$$ The Wavelet Transform Wf of a function f(t) is computed by taking the inner product of function f(t) with the translated and dilated versions of mother wavelet.
For small values of s, \(\psi_{k,s}\) will be of shorter duration and higher frequency. For large value of s, \(\psi_{k,s}\) it will be more spread out in time and will consist of low frequencies. The fact that wavelet functions are bandpass functions ensures that we cannot cover the entire frequency spectrum just with the wavelet functions.To solve this problem, scaling functions \(\phi(t)\) are introduced. They are complement of wavelet functions and correspond to low pass filter in signal processing terms.
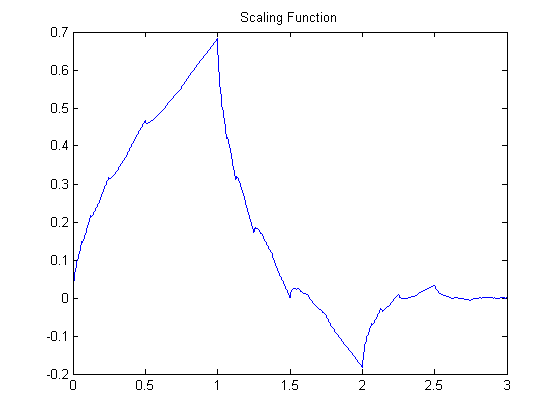
Db2 Scaling Function
Below is an example of Daubechies2 wavelet [blue] being scaled by \(a=1/2\).The scale \(a\) is inversely proportional to frequency. Small scale values [ \(0 < a < 1\) ] correspond to high frequencies while large scale values [ \( a > 1 \) ] to low frequencies. The second figure shows the same mother wavelet[blue] being shifted by \(b=20\).
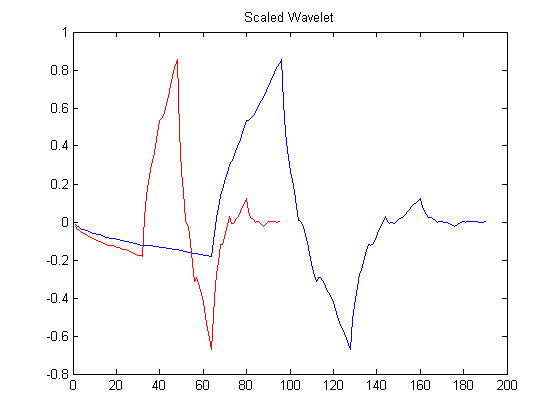
Db2 Wavelet Scaling Demo
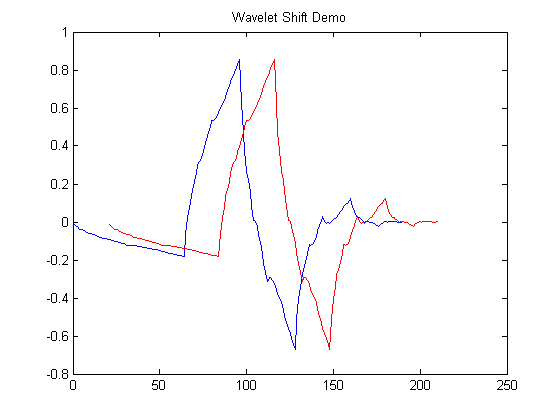
Db2 Wavelet Shift Demo
Wavelet Transform, so defined, happens to be computationally unwieldy as translations and dilations can take any value. A better approach is to discretize translation and dilation steps. Mathematically, let \(s=a^{m}\) and \(k=a^{m}n\) where m and n are integers.
$$\psi_{m,n}(t)=a^{\frac{-m}{2}}\psi(a^{-m}t-n)$$Wavelet Properties
- 1. Vanishing Moments: A wavelet of \(n\) vanishing moments is orthogonal to polynomials of degree \(n-1\). All polynomials of degree less than \(n\) will get filtered out when they are processed by wavelet \(\psi(t)\) \[ \int_{-\infty}^{\infty} t^{k} \psi(t) dt = 0 , for (0 \le k < n) \] For a given scaling function and wavelet derived from low pass filter \(h(n)\), number of vanishing moments depends solely on number of zeros at \(\omega=\pi\). In other words, its transfer function and its \(n-1\) derivatives in frequency( or \(z\)) domain vanish at \(\omega=\pi\)\((z=-1)\).
- 2. Regularity: of a wavelet is related to differentiability of a wavelet in the frequency domain. More regularity corresponds to smoother wavelet and more vanishing moments. Scaling filter is \(N\) regular if it has \(N\) zeros at \(\omega=\pi\). For more on local and global regularity, refer to books by Daubechies and Mallat.
- 3. Admissibility condition is given by \[ \int_{-\infty}^{\infty} \frac{|\psi(\omega)|^{2}}{|\omega|} d \omega < \infty \] Wavelets being band pass functions is an implication of admissibility condition.
- 4. Compact Support: Wavelets should ideally have compact support. Like other properties, this property too depends on the low pass filter \(h\).
- 5. Symmetry: Certain wavelets , eg. biorthogonal wavelets , are designed to be symmetric. These are specially useful in image processing applications.
- 6. Orthogonality: With the exception of Haar wavelets, wavelets can't be both symmetric and orthogonal so the choice usually comes down to specific applications and requirements.
