Filterbanks and Wavelets
As mentioned in the previous chapter Discrete Wavelet Transform can be obtained by iterating over low pass filters of a given filter bank.
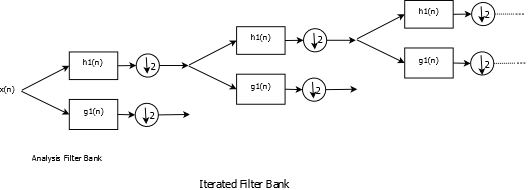
Iterated Analysis Filter Bank
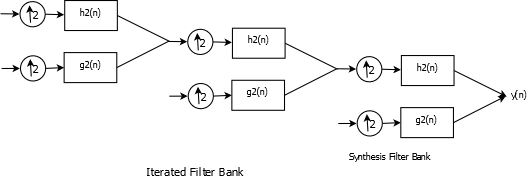
Iterated Synthesis Filter Bank
Let us consider one stage filtering and downsampling in the analysis filter bank. Downsampling is needed in order to get rid of redundancy as , say, a 1000 point input sample results in two ~1000 point outputs after filtering. We downsample by two in order to keep the signal samples at ~1000. Similarly at the synthesis bank, we first upsample the wavelet coefficients by 2 before filtering. Filter have to be designed appropriately in order to ensure that the signal reconstruction is perfect. Filter choices also effect wavelet shape as will be demonstrated shortly.
Recall the dilation and wavelet equations.
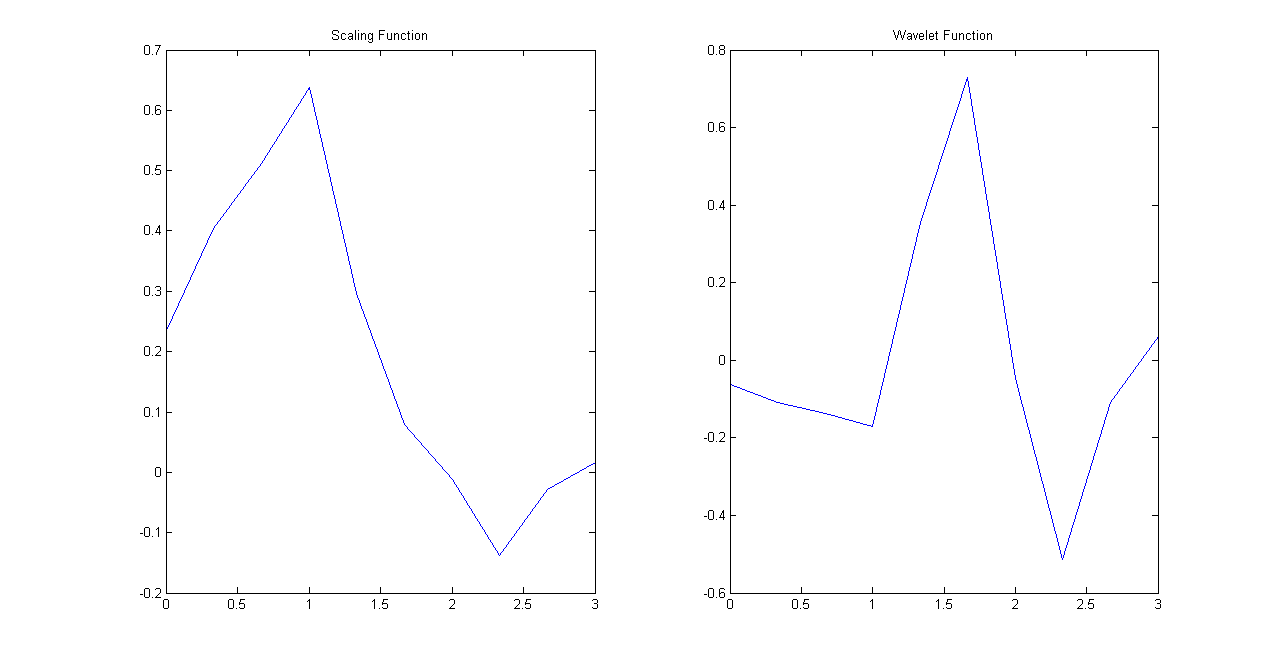
\[ \phi(t)=2\sum_{k} h(k)\phi(2t-k) \] \[ \psi(t)=2\sum_{k} g(k)\phi(2t-k) \] If we iterate over these equations then the iteration can be written as \[ \phi^{(i+1)}(t)=2\sum_{k} h(k)\phi^{(i)}(2t-k) \]Keep in mind that both wavelet and dilation equations will end up getting iterated over \(\phi(t)\) where \(\phi^{(0)}(t)\) is the box function \([1,1]\). If the functions converge then we should be able to get wavelet and scaling functions in few steps. In the example below Daubechies's db2 wavelet and scaling filters were iterated to yield wavelets and scaling functions in five iterations.
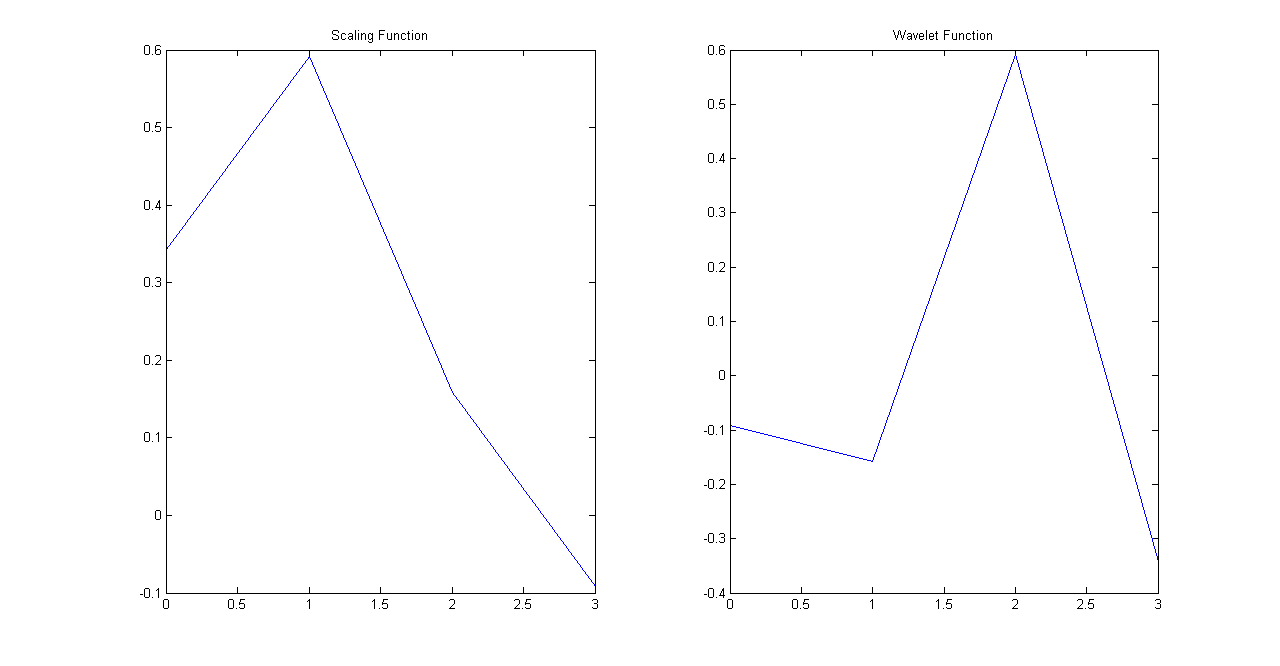
Db2 4-tap Low Pass and High pass Filters
Scaling and Wavelet Function Iteration #1

Scaling and Wavelet Function Iteration #2
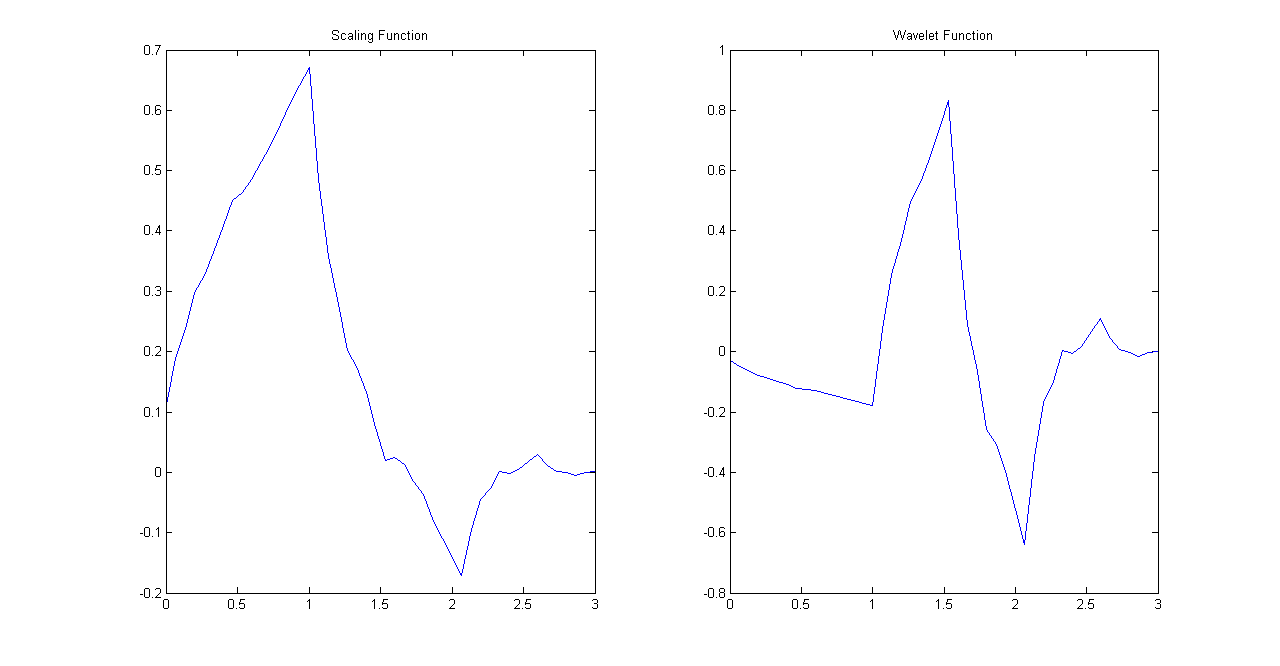
Scaling and Wavelet Function Iteration #3
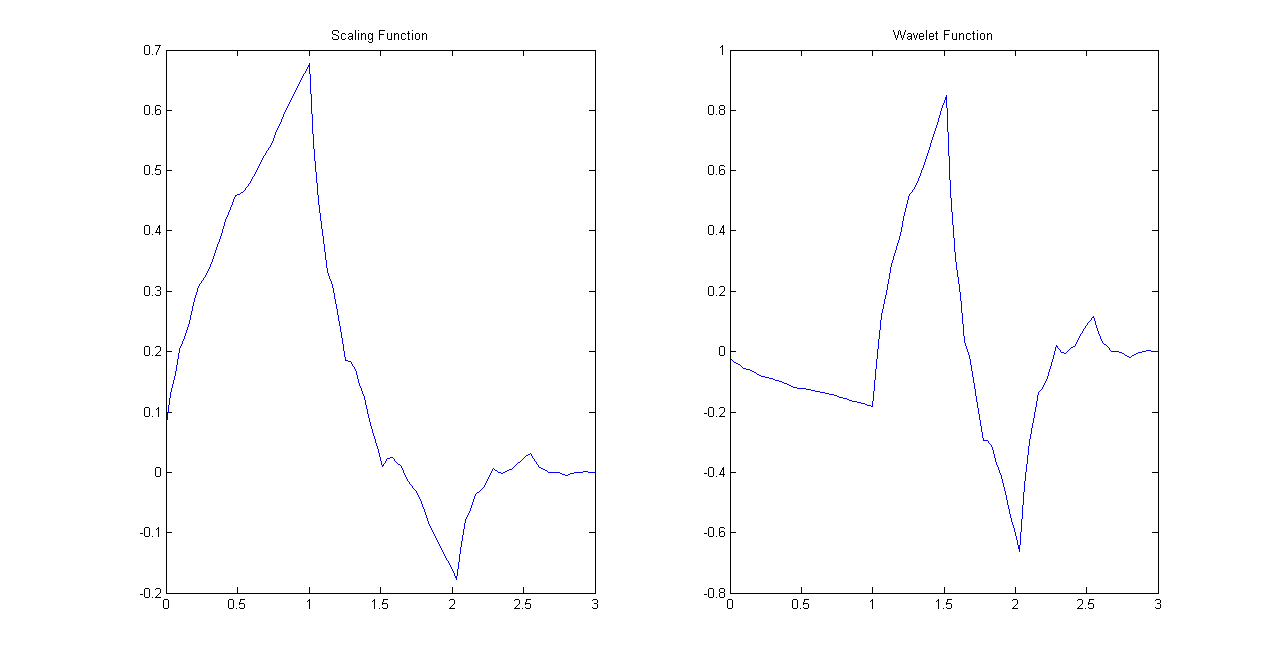
Scaling and Wavelet Function Iteration #4
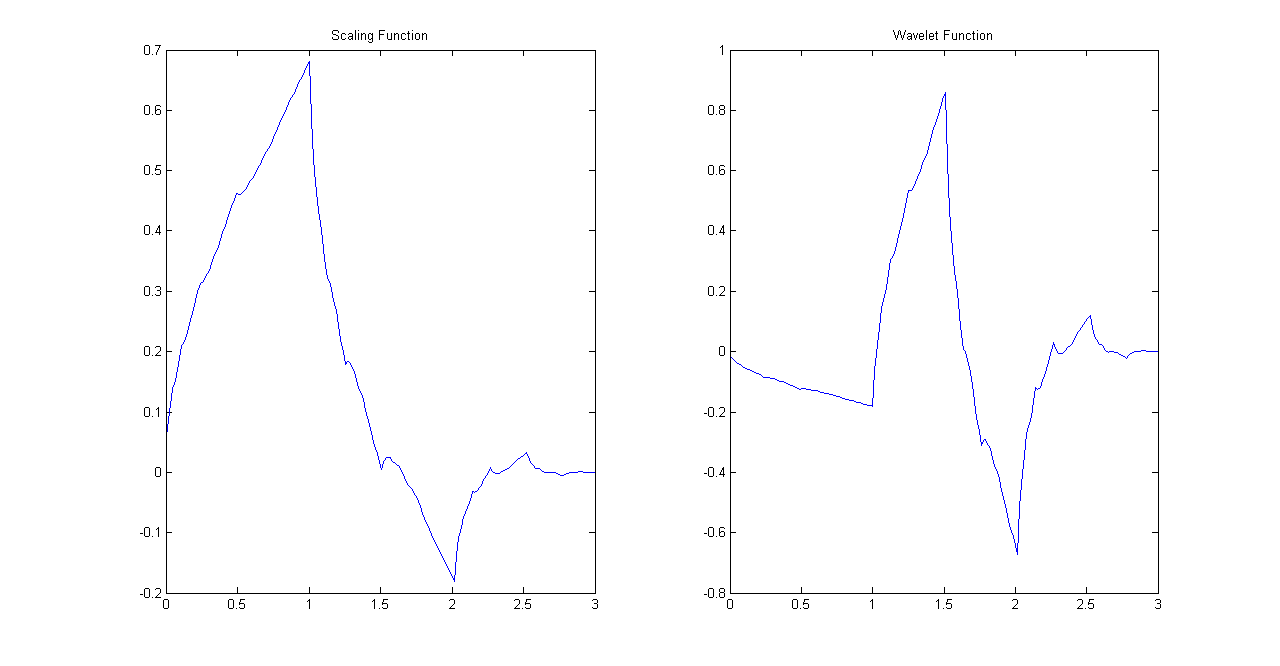
Scaling and Wavelet Function Iteration #5
Orthonormal Discrete Wavelet Transform
In terms of scaling and wavelet functions we have three orthonormality equations at a given scale \(j\)
\[ <\phi_{j,k},\phi_{j,l}>= \int_{-\infty}^{\infty} 2^\frac{j}{2} \phi(2^{j}t-k)2^\frac{j}{2} \phi^{*}(2^{j}t-l)dt=\delta(k-l) \] \[ <\psi_{j,k},\psi_{j,l}>= \int_{-\infty}^{\infty} 2^\frac{j}{2} \psi(2^{j}t-k)2^\frac{j}{2} \psi^{*}(2^{j}t-l)dt=\delta(k-l) \] \[ <\phi_{j,k},\psi_{j,l}>= \int_{-\infty}^{\infty} 2^\frac{j}{2} \phi(2^{j}t-k)2^\frac{j}{2} \psi^{*}(2^{j}t-l)dt=0 \]Derivation is straightforward. If \(h_{1}\) and \(g_{1}\) are low pass and high pass filters respectively then, in an orthonormal filter bank, their inner product is zero. Use dilation equations, take inner product of scaling and wavelet functions. Notice that it can be expressed in forms of \(h_{1}\) and \(g_{1}\) and that these two are orthonormal filters satisfying orthonormality properties.
Discrete Wavelet Transform requires that four filters be designed- two for analysis bank and the other two for synthesis bank. However, perfect reconstruction imposes conditions on filters such that no more than two filters are enough to design a DWT Multiresolution Analysis. In case of Orthogonal DWT, only one filter is sufficient as the other three filters can be obtained from the prototypical low pass filter. More on this will follow after discussion of Biorthogonal wavelets.The analysis high pass filter is the mirror image (alternate flip) of low pass filter while synthesis filters are transposes of analysis filters.For a given \(N+1\)-tap low pass analysis filter \(H_{1}(z)\), the other three filters are
High Pass Analysis Filter \(H_{2}(z) = -z^{-N}H_{1}(z)\) Low Pass Synthesis Filter \(G_{1}(z) = H_{2}(-z)\) High pass Synthesis Filter \(G_{2}(z) = -H_{1}(-z)\)
Biorthogonal Discrete Wavelet Transform
We get biorthogonal wavelets from biorthogonal filters. Biorthogonal analysis filters are not orthogonal to each other but the analysis filters and synthesis filters are orthogonal with respect to each other. Consider a two-channel biorthogonal filter bank.
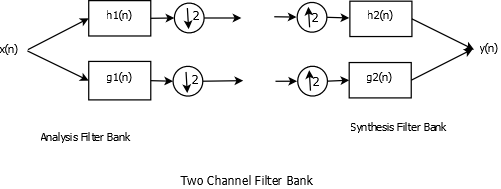
Two Channel Biorthogonal Filter Bank
In case of orthonormal filter banks we had three orthonormality equations. In case of biorthogonal filter banks, we have four equations. In filter bank terms, these four equations are
\[ \lt h_{1}(n),h_{2}(2k-n) \gt=\delta(k) \] \[ \lt g_{1}(n),g_{2}(2k-n) \gt=\delta(k) \] \[ \lt h_{1}(n),g_{2}(2k-n) \gt=0 \] \[ \lt g_{1}(n),h_{2}(2k-n) \gt=0 \]Biorthogonal Multiresolution Analysis
In biorthogonal case, \(V_{j+1}=V_j\oplus W_j\) is still valid but \(V_j\) and \(W_j\) are not orthogonal complements. This necessitates introduction of another complementary multiresolution space. It is usually denoted by \(\widetilde{V}_j\) and \(\widetilde{W}_j\) such that
\[ \widetilde{V}_{j+1} =\widetilde{V}_j +\widetilde{W}_j \] The relationship between ``normal'' MRA and ``Tilde'' MRA is crucial as it defines biorthogonality \[ \widetilde{V}_j \bot W_j \] \[ V_j \bot \widetilde{W}_j \]``Tilde'' MRA is usually associated with analysis filter bank while the ``normal'' MRA is associated with synthesis filter bank. Therefore \(\widetilde{\phi}\) and \(\widetilde{\psi}\) are analysis scaling and wavelet functions while \(\phi\) and \(\psi\) are synthesis scaling and wavelet functions, respectively. We also have two sets of dilation equations in this case.
Analysis Dilation Equations
\[ \widetilde{\phi}(t)=2\sum_{k} \widetilde{h}(k)\widetilde{\phi}(2t-k) \] \[ \widetilde{\psi}(t)=2\sum_{k} \widetilde{g}(k)\widetilde{\phi}(2t-k) \]Synthesis Dilation Equations
\[ \phi(t)=2\sum_{k} h(k)\phi(2t-k) \] \[ \psi(t)=2\sum_{k} g(k)\phi(2t-k) \]In terms of scaling and wavelet functions we have four biorthogonality equations at a given scale \(j\)
\[ <\phi_{j,k},\widetilde{\phi}_{j,l}>= \int_{-\infty}^{\infty} 2^\frac{j}{2} \phi(2^{j}t-k)2^\frac{j}{2} \widetilde{\phi}^{*}(2^{j}t-l)dt=\delta(k-l) \] \[ <\psi_{j,k},\widetilde{\psi}_{j,l}>= \int_{-\infty}^{\infty} 2^\frac{j}{2} \psi(2^{j}t-k)2^\frac{j}{2} \widetilde{\psi}^{*}(2^{j}t-l)dt=\delta(k-l) \] \[ <\widetilde{\phi}_{j,k},\psi_{j,l}>= \int_{-\infty}^{\infty} 2^\frac{j}{2} \widetilde{\phi}(2^{j}t-k)2^\frac{j}{2} \psi^{*}(2^{j}t-l)dt=0 \] \[ <\widetilde{\psi}_{j,k},\phi_{j,l}>= \int_{-\infty}^{\infty} 2^\frac{j}{2} \widetilde{\psi}(2^{j}t-k)2^\frac{j}{2} \phi^{*}(2^{j}t-l)dt=0 \]These four equations can be proved by plugging dilation equations into the left hand side (inner products). The decomposition and reconstruction proof is similar to the orthogonal MRA case.(more on next page......)
