Complex Wavelet transform

Motivation for Complex Wavelet Transform

Discrete Wavelet Transform has many advantages over Fourier Transform with main advantage that it can do localized analysis but there are other areas where DWT lags behind Fourier Transform. Shift Variance is one of those areas. Fourier Transform is shift invariant which is a desirable property but the use of downsampling makes DWT prone to shift variance as can be seen in the figure below. An impulse loacted at \(n=51\) results in a different response than one located at \(n=80\) with responses being computed at level one of decomposition with a Db8 wavelet DWT filter bank. Not only the two wavelet coefficients are different, the second set of coefficients contain nearly \(20\%\) more energy than the first .Keep in mind that DWT can be made nearly shift invariant by removing downsamplers but it makes DWT ``significantly'' redundant.

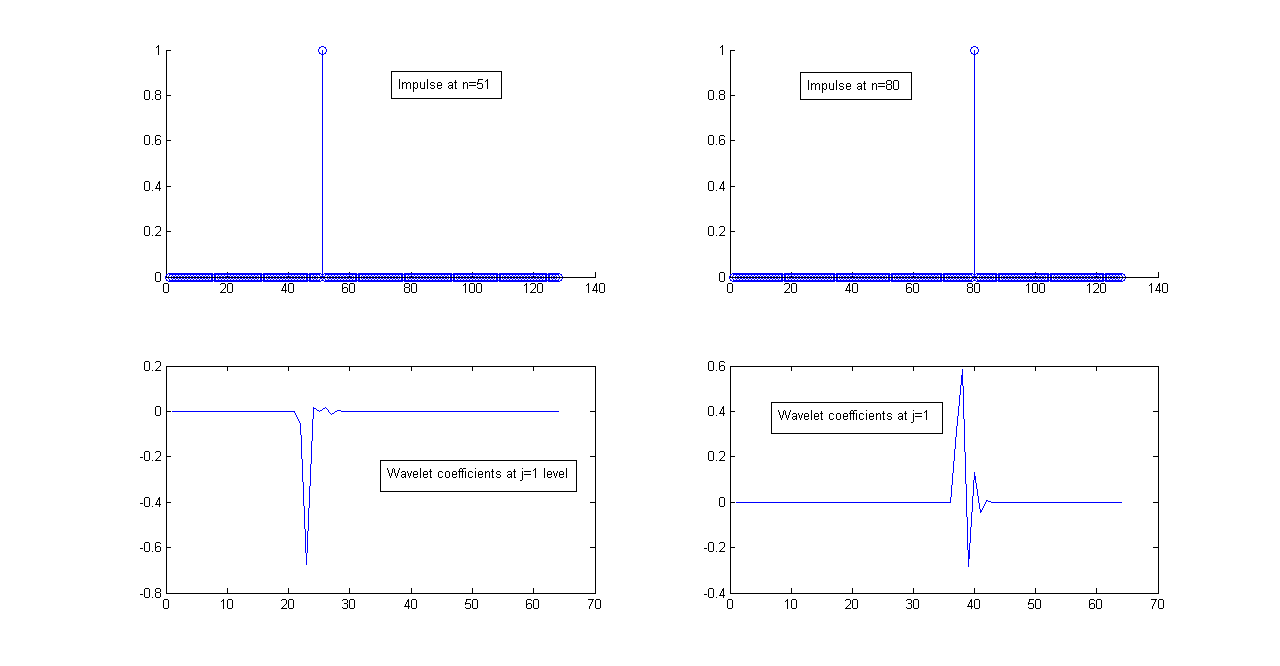
DWT Shift Variance Demonstration

Directionality is another issue with regular DWT. As seen with 2D DWT, it is only good in horizontal and vertical direction. While DWT can isolate diagonals with the High-High band it cannot distinguish between signal elements aligned at \(45^{\circ}\) and \(135^{\circ}\).

Some other issues with real-valued DWT are absence of any phase information and aliasing that may be present because of quantization errors etc. which may not allow perfect reconstruction of signal.

Hilbert Transform and Analytic Signal

\[ F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-j\omega t} d \omega \]

Fourier Transform consists of two 90\degree out of phase sine and cosine terms. It can represented as

\[ e^{-j\omega t}=cos(\omega t)+j sin(\omega t) \]

In order to develop complex wavelets that are analogous to Fourier Transform, it is important to take a look at Analytic signals and Hilbert Transform.

An Analytic signal \(x_{a}(t)\) is defined as

\[ x_{a}(t)=g(t)+j\widehat{g}(t) \]

where \(g(t)\) is a real valued signal while \(\widehat{g}(t)\) is the \(90^{\circ}\) out of phase version of \(g(t)\). We use Hilbert transform to generate \(\widehat{g}(t)\). Hilbert transform of a signal \(g(t)\) is given by

\[ \widehat{g}(t)=H(g(t))=\frac{1}{\pi} \int_{-\infty}^{\infty} \frac{g(t)}{t-\tau} d \tau \]

Taking Fourier Transform, we get

\[ \widehat{G}(\omega)= -j Sgn(\omega) G(\omega) \]

where \[ sgn(\omega)=1 , \omega \gt 0 \] \[ sgn(\omega)=-1, \omega \lt 0 \]

Since \(x_{a}(t)\) is a complex signal, its magnitude and angle are given by \[ \|x_{a}(t)\|=\sqrt{g(t)^{2}+\widehat{g}(t)^2} \] \[ \angle x_{a}(t)= tan^{-1} \left[\frac{\widehat{g}(t)}{g(t)}\right] \]

Another very important property of analytic signal is that it only exists for positive frequencies.

\[ X_{a}(\omega)=(1+ Sgn(\omega)) G(\omega) \] \[ X_{a}(\omega)= 2G(\omega), \omega \gt 0 \] \[ X_{a}(\omega)= G(\omega), \omega = 0 \] \[ X_{a}(\omega)= 0, \omega \lt 0 \]

This helps reduce bandwidth use by the signal and reduces aliasing.

Complex Valued Wavelet Coefficients

Let \(\psi_{A}(t)\) be the analytic wavelet and let \(\psi_{R}(t)\) and \(\psi_{I}(t)\) be its real and imaginary terms where

\(\psi_{I}(t)=H(\psi_{R}(t))\). \[ \psi_{A}(t)=\psi_{R}(t)+j \psi_{I}(t) \]

The wavelet coefficients at level \(j\) can be given by

\[ W_{a}(j,n)=W_{r}(j,n)+j W_{i}(j,n) \]

The magnitude and angles are, therefore,

\[ \|W_{a}(j,n)\|=\sqrt{W_{r}(j,n)^{2}+W_{i}(j,n)^{2}} \] \[ \angle W_{a}(j,n)= tan^{-1} \left[\frac{W_{i}(j,n)}{W_{r}(j,n)}\right] \]

As can be seen, the wavelet coefficients( as well as scaling coefficients) are complex but, like Fourier transform, they can be used to analyze complex as well as real signals. Complex wavelets can be implemented with filter banks but ,in this case, the implementation will involve two filter banks , with one corresponding to the real wavelet while the other corresponding to complex. Compared to decimated DWT this Dual-Tree Complex wavelet Transform is redundant.

Dual-Tree Complex Wavelet Transform

As mentioned,the idea is to have two sets of analysis and synthesis filter banks in quadrature with each other.

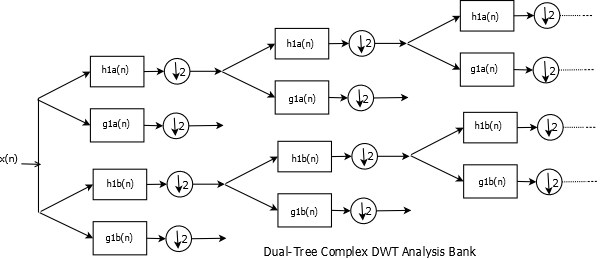
Complex DWT Analysis Bank

Complex DWT Synthesis Bank

On the analysis side, filters \(h_{1a}\),\(h_{1b}\),\(g_{1a}\) and \(g_{1b}\) are all real filters but they are designed so that \(h_{1a}\) and \(g_{1a}\) are in quadrature. Same is true for high pass filters \(h_{1b}\) and \(g_{1b}\). Let \(\psi_{a}(t)\) and \(\psi_{b}(t)\) be the wavelets associated with the two branches then they need to be designed so that

\[ \psi_{b}(t)=H[\psi_{a}(t)] \]

This is in addition to the perfect reconstruction conditions the filter banks have to fulfill. The additional Hilbert Transform means that normal DWT implementations (eg., Daubechies's construction) won't work and filters need to be designed from scratch.

Hilbert Transform condition

Using dilation equations, the scaling function and wavelet for top branch (real) can be written as

\[ \phi_{a}(t)=2 \sum_{n} h_{1a}(n) \phi(2t-n) \] \[ \psi_{a}(t)=2 \sum_{n} g_{1a}(n) \phi(2t-n) \]

Assuming that these two filters are orthonormal, the high pass filter can be expressed as alternating flipped version of low pass filter.

\[ g_{1a}(n)=(-1)^{n} h_{1a}(d-n) \]

Furthermore, Selesnick showed that if the two low pass filters in the analysis filter bank are half sample shifted version of other, the wavelet functions obtained by iterating the related high pass filters will be Hilbert transform pair. In other words,

\[ h_{1b}(n) \approx h_{1a}(n-0.5) \Rightarrow \psi_{b}(t) \approx H[\psi_{a}(t)] \]

In Fourier Domain, it translates to a difference of \(0.5 \omega\) while the magnitudes of two filters are equal. A true half-sample shifted system isn't practically realizable so \(\psi_{b}(t)\) and \(\psi_{a}(t)\) are only approximately realizable.

Filter Design Methods

1. Linear Phase Biorthogonal Filters: Low pass filter \(h_{1a}(n)\) is chosen to be even length \(N\) symmetric filter while the other low pass filter(complex branch) \(h_{1b}(n)\)is chosen to be odd length \(N-1\) symmetric filter. It is seen that the phase difference between the two filters is \(-0.5N\omega-(-0.5(N-1)\omega)= -0.5\omega\) which satisfies the half sample-shifted phase condition but magnitude isn't necessarily equal. We can however design filters so that the magnitudes of two low pass filters are roughly equal.
2. Q-Shift Design: Using quarter-shift method, the low pass filters are related as following \[ h_{1b}(n)=h_{1a}(N-1-n) \]

where \(h_{1a}(n)\) filter length \(N\) is even. As can be see that this low pass filter configuration has both filters having same magnitude but they don't automatically satisfy the half sample-shifted phase condition. Fourier domain frequency response of \(H_{1b}(\omega)\) can be written as

which corresponds to following phase response

Since the two filters are supposed to satisfy the half sample-shifted condition

Solving for \(H_{1a}(\omega)\), we get

Two observations:

i. Low Pass Filter \(H_{1a}(\omega)\) is approximately symmetric.
ii. There is a quarter-shift element( It is shifted by 0.25 from the natural symmetric point) present that makes the equation not fully symmetric.

The analytic wavelets in this case have real and imaginary values that are time reversed version of each other.Since the filters are even and almost symmetric, orthonormal solutions are possible unlike in the first case.

3. Selesnick's Method: In his 2002 paper, Selesnick suggested following design for the two low pass filters. \[ H_{1a}(z)=F(z)D(z) \] \[ H_{1b}(z)=F(z)z^{-L}D(z^{-1}) \] where \(D(z)\) is chosen such that the half sample shifted condition is satisfied. \[ H_{1b}(z)=H_{1a}(z) \frac{z^{-L}D(z^{-1})}{D(z)} \] Observe that \[ A(z)=\frac{z^{-L}D(z^{-1})}{D(z)} \] is an all pass filter which makes the magnitudes of \(H_{1a}(z)\) and \(H_{1b}(z)\) equal. \(A(z)\) needs to be designed so that the two low pass filters are half sample shifted. For more on these filters and their implementations, see the references(Resources).