Iterated Filter Banks
Noble Identities
Noble Identities are utilized in multirate systems to reverse the order of resampling and filtering.
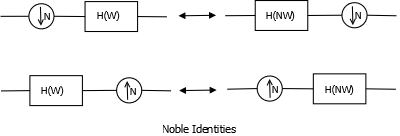
Noble Identities
The first row shows the noble identity of downsampling while the second one shows upsampling. Downsampling by \(N\) followed by a filtering operation with \(H(\omega)\) is equivalent to filteing with an \(N\)-interpolated version \(H(N\omega)\) and then downsampling by \(N\). Noble identities can be utilized to make computation more efficient or to simplify a multi stage multirate system.
Iterated Filter Banks
In the classical Discrete Wavelet transform algorithm, Iterated filter banks are constructed by iterating over low pass channels of a two-channel filter bank.Other constructions are also possible depending on specific needs but I will concentrate on Low Pass iterations for obvious reasons.
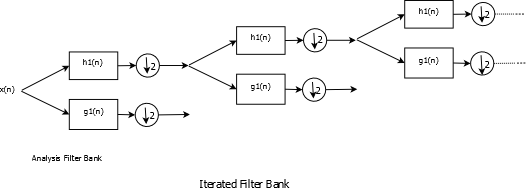
Analysis Filter Bank
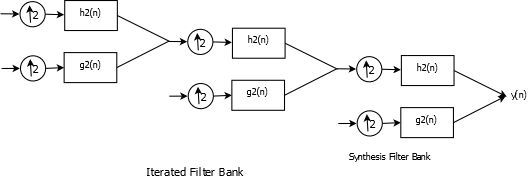
Synthesis Filter Bank
Using Noble Identities it can be shown that iterating over J stages of two-channel analysis filter bank is equivalent to filtering by \(\prod_{n=0}^{J-1}H(2^{n}\omega)\) or in terms of \(Z-\)transform \(\prod_{n=0}^{J-1}H(z^{2^{n}})\) and then downsampling by \(2^{J}\). The process works in reverse in synthesis case.
